Musik, die Fibonacci Reihe und der Goldene Schnitt

Musikalische Reihen beziehen sich auf Fibonacci-Zahlen. Auf der Klaviertastatur ist deutlich erkennbar, daß Musik auch etwas mit der Fibonacci-Reihe zu tun hat. Die Fibonacci-Reihe findet sich in allen fundamentalen Aspekten von Kunst, Schönheit und Leben wieder. Auch die Musik hat eine Basis in der Reihe, wie:

• Es gibt 13 Noten in der Spanne einer Note durch ihre Oktave.
• Eine Tonleiter besteht aus 8 Noten, von denen die
• 5. und 3. Noten die Grundlage für alle Akkorde bilden,
• basierend auf einem Intervall zwischen zwei Tönen, deren Frequenzen sich wie 2:1 verhalten.

Die Oktave auf der Klaviertastatur von C bis C hat 13 Tasten. 8 weiße Tasten und 5 schwarze Tasten, die in Gruppen von 3 und 2 aufgeteilt sind. Jetzt bemerken einige, dass es ja nur 12 “Noten” in der Reihe gibt. Wenn es keine Möglichkeit gibt Anfang und Ende festzuhalten, dann kann man auch nicht die Abstufungen dazwischen berechnen. Somit ist die 13. Note als Oktave für die Berechnung der Frequenzen der anderen Noten wesentlich.

Das Wort „Oktave“ kommt aus dem Lateinischen für 8 und bezieht sich auf die acht Töne der gesamten Tonleiter, die in der Tonart C – “C-D-E-F-G-A-H-C” sind. In einer Tonleiter ist die dominante Note die 5. Note der Dur-Tonleiter, die auch die 8. Note aller 13 Noten ist aus denen die Oktave besteht. Dies bietet eine zusätzliche Instanz von Fibonacci-Zahlen in wichtigen musikalischen Beziehungen.

Interessanterweise ist 8/13 = .61538, was ungefähr Phi, dem Goldenen Schnitt entspricht. Darüber hinaus besteht der typische Dreiklang (Terz) in der Tonart A aus A, seinem Fibonacci & phi-Partner E und D, zu dem A die gleiche Beziehung wie E zu A hat. Dies ist analog zur Basis „A ist zu B wie B zu C“ für den Goldenen Schnitt, oder in diesem Fall „D ist zu A wie A zu E“.

Nummeriere zunächst die 8 Noten der Oktav Tonleiter. Als nächstes nummeriere die 13 Noten der chromatischen Tonleiter. Die auf beiden Tonleitern rot dargestellten Fibonacci-Zahlen fallen bei beiden Methoden (C, D, E, G und C) auf dieselbe Tonart. Dies erzeugt die Fibonacci-Verhältnisse von 1:1, 2:3, 3:5, 5:8 und 8:13.

Musikfrequenzen basieren auf Fibonacci-Verhältnissen

Noten in der Skala der westlichen Musik basieren auf natürlichen Harmonien die durch Frequenzverhältnisse erzeugt werden. Die in den ersten sieben Ziffern der Fibonacci-Reihe gefundenen Verhältnisse (0, 1, 1, 2, 3, 5, 8) beziehen sich auf die Schlüsselfrequenzen von Noten.

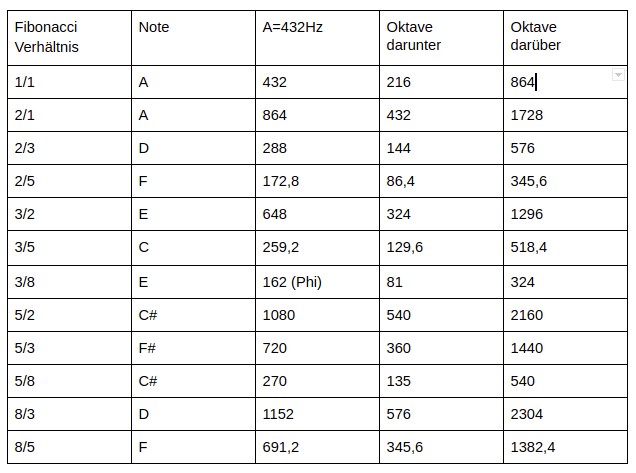
Die oben berechnete Frequenz beginnt mit A = 432Hz und wendet die Fibonacci-Beziehungen an. In der Praxis werden Klaviere auf eine „temperierte“ Frequenz gestimmt. Eine künstliche Anpassung die entwickelt wurde, um beim Spielen in verschiedenen Tonarten eine verbesserte Tonalität zu erzielen. Beim anzupfen einer Gitarre entstehen harmonische Frequenzen in der sich reine Fibonacci Beziehungen widerspiegeln.

A=432 Hertz wurde von klassischen Komponisten verwendet und führt zu einer Abstimmung der gesamten Frequenz. Diese ist mit Zahlen verbunden, wie sie beim Bau einer Vielzahl von antiken Werken und heiligen Stätten wie zum Beispiel der Großen Pyramide von Ägypten verwendet wurden.